Systemy pomiarowe przebyły bardzo długą drogę do obecnej, bardzo poręcznej formy oprogramowania, które działa na każdym komputerze, zastępując skrzynkę pokazującą wykres fazy, skrzynkę pokazującą wykres amplitudy i odpowiedzi impulsowej. Żeby jednak zrozumieć, jak poszczególne segmenty działają i skąd biorą wynik, potrzebna jest nam wiedza na temat czysto matematycznego zagadnienia, a mianowicie analizy harmonicznej. Podstawowym narzędziem matematycznym w analizie harmonicznej jest transformacja Fouriera, która pozwala określić ilości, amplitudy i fazy składowych częstotliwości.
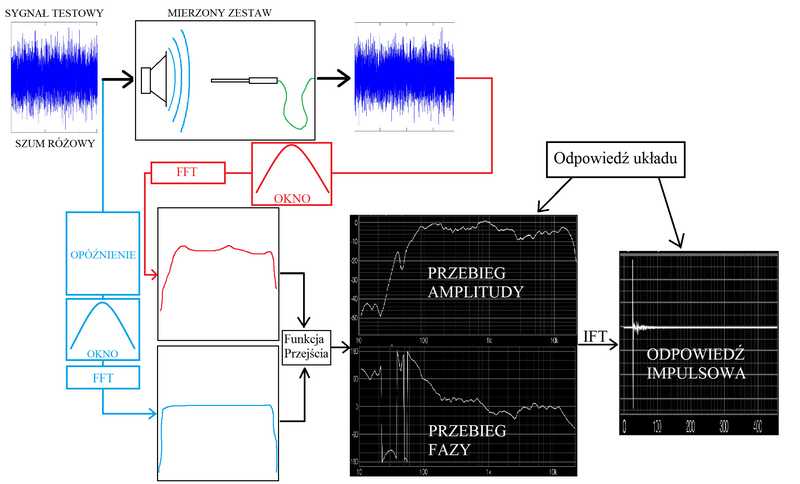
Schemat typowego systemu pomiarowego opartego o dwa kanały FFT. Systemy pomiarowe przebyły bardzo długą drogę do obecnej, bardzo poręcznej formy oprogramowania, które działa na każdym komputerze, zastępując skrzynkę pokazującą wykres fazy, skrzynkę pokazującą wykres amplitudy i odpowiedzi impulsowej. Żeby jednak zrozumieć, jak poszczególne segmenty działają i skąd biorą wynik, potrzebna jest nam wiedza na temat czysto matematycznego zagadnienia, a mianowicie analizy harmonicznej. Podstawowym narzędziem matematycznym w analizie harmonicznej jest transformacja Fouriera, która pozwala określić ilości, amplitudy i fazy składowych częstotliwości. Dla tych, którzy nigdy nie mieli do czynienia z zagadnieniem, postaram się zobrazować, czym jest wyżej wymieniona operacja bez podawania wzorów i przykładów obliczeń. Następnie przejdziemy do tematu samych systemów pomiarowych, czyli tego, jakie urządzenia wyróżniamy i skąd biorą się w nich wyniki. Transformacja Fouriera – brzmi groźnie, choć poziom skomplikowania różni się w zależności od tego, czy chcemy poznać, czym jest lub jak się ją liczy. Obliczenia prostych transformacji wymagają znajomości analizy matematycznej na poziomie 1 może 2 – jeśli nie zamierzamy liczyć podwyższonej liczby wymiarów dla przypadku. Na potrzeby artykułu pozostaniemy przy opisie tego, skąd bierze się wynik. W pierwszej kolejności przyjmijmy określenie wypadkowej, czyli tak naprawdę elementu badanego za pomocą transformacji Fouriera. Wypadkowa jest sumą składowych częstotliwości, jak wspomniałem w jednym z poprzednich artykułów, każdą składową możemy opisać za pomocą wektorów i tak samo jak wektory sumować. Nie rozwiniemy tematu od strony algebraicznej, lecz ze względu na dobro czytelnika przedstawię intuicyjny, geometryczny sposób na zrozumienie, jak nasze składowe przyczyniają się do powstania wypadkowej.Zamiana sygnału w postaci przebiegu czasowego na charakterystykę amplitudową. Na początek wyobraźmy sobie jedną częstotliwość o pewnej amplitudzie przedstawioną za pomocą strzałki z początkiem w zerze dwuwymiarowego układu współrzędnych, gdzie długość strzałki określać będzie amplitudę, a czas obiegu o 360 stopni wyznaczy częstotliwość. Trzecim wymiarem dla naszego układu będzie czas upływający pod kątem prostym do płaszczyzny X,Y. Jeśli w tej chwili zaczniemy obracać naszym wektorem i odliczać czas, obraz rysowany przez koniec wektora będzie spiralą. Tak właśnie narodził się wykres funkcji sinus i cosinus. Ktoś pewnie zapyta – ale jak? skąd? Weź rozciągniętą sprężynę (lub po prostu sprężynę rozpychającą), zamontuj ją nieruchomo i oświetl latarką prostopadle do jej osi, a następnie przemieść źródło światła po promieniu o 90 stopni i ponownie spójrz na cień rzucany przez sprężynę. Zauważysz dwa wykresy przesunięte względem siebie o 90 stopni – jak w przypadku sinusoidy i wykresu funkcji cosinus (rys. 1.).Gdy wiemy już, skąd wzięła się sinusoida, pora na powrót do określenia „wypadkowa” i zapoznania się z tym, jak sygnał widzi matematyk lub nasz system pomiarowy wyposażony w analizę FFT. Przede wszystkim pojedynczy sinus jest niczym innym jak wyżej wspomnianym wektorem obracającym się wokół osi Z (rys. 1.), wraz z upływem czasu wektor kreśli spiralę, której rzut jest znanym już nam przebiegiem. Dokładając kolejną częstotliwość do poprzedniej, nakładamy następny wektor na koniec poprzedniego, z tą różnicą, że kręci się on wraz z pierwszym i dodatkowo wokół własnej osi leżącej na końcu pierwszego, jeśli reprezentowana przez niego częstotliwość jest inna niż częstotliwość pierwszego. Drugi wektor jest jakby przytwierdzony na końcu pierwszego, tak aby przy wspomnianej różnicy częstotliwości mógł kreślić koła o promieniu równym swojej długości. Cały układ wiruje wraz z wektorem pierwszym, kreśląc zwykłą spiralę, gdy częstotliwości są równe, lub „spiralną spiralę”, gdy się różnią. Oba wektory zaczynają swą drogę z pewną amplitudą i początkową fazą, a o amplitudzie wypadkowej decyduje chwilowa wartość względem zera i położenia końca drugiego wektora. Tym sposobem dodawać można kolejne częstotliwości i w każdej chwili poznać wartość wypadkową.







